Relative air density and fuelling
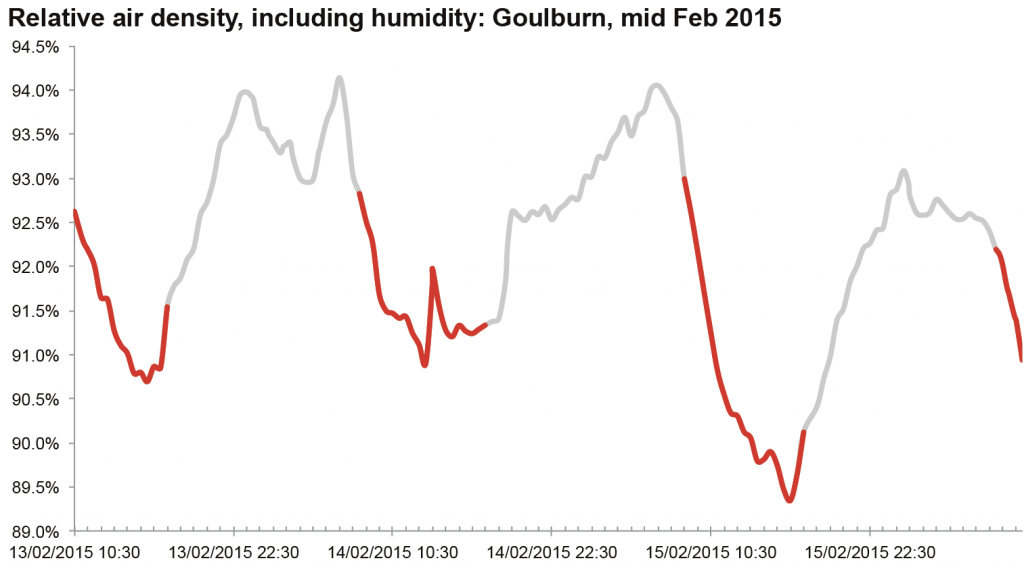
Top image: an example of relative air density, charted for a few days at Goulburn (original data source is the Bureau of Meterology). Red segments are the rough daytime values: note how much it varies even during the day, but also how it varies between days.
The amount of fuel required for maximum power or perfect combustion (rarely equal!) relates to the amount of oxygen available. The amount of oxygen available depends on the density of the atmosphere where you are. This is going to be a technical article, for which I apologise, but I’m also working on some simple calculators to help out with air density.
tl;dr: air density matters especially for 2 strokes, and you gotta understand it to get the best out of your machine. You can buy meters to deal with it, but you can also calculate it from cheap weather stations or even BoM data.
Air density basics
As discussed above, the air density varies. It varies according to the following:
- Altitude
As you go up in altitude, the actual air pressure around you changes. This is not a huge problem in Australia where we have at most 2000 m of elevation, but if your motorbike is highly tuned you’ll definitely see a difference in jetting required at sea level versus, say, Wakefield Park at Goulburn (~650 m elevation).
The practical effect of this?
As you go higher in altitude, your jetting needs to be leaner as there’s less oxygen available due to the lower density; conversely
As you go lower in altitude, your jetting needs to be richer as there’s more oxygen available due to the higher density.
- Temperature
As the temperature increases, the density of the air decreases (as the gas gets a bit more excited, it takes up more volume for the same mass).
As the temperature increases, your jetting needs to be leaner;
As the temperature decreases, your jetting needs to be richer. - Air pressure
As the air pressure increases, the density of the air increases. So, if you’re in the middle of a high pressure system then you’ve got higher air density; if you’re in the eye of a cyclone it’s going to be a bit lower (if we want to think of extremes).
As the air pressure decreases, your jetting needs to be leaner;
As the air pressure increases, your jetting needs to be richer. - Humidity
Humidity is the final factor. Some of the air pressure is coming from the ‘vapour pressure’ of the water in the atmosphere (100% humidity means you’ve got as much water vapour that the air can hold at that current temperature).
As the humidity increases, your jetting needs to be leaner (as you have less overall oxygen, as the ‘dry mass’ of air has decreased as it’s offset by the humidity);
As the humidity decreases, your jetting needs to be richer.
NOTE: Rarely do air density meters take into account the effects of humidity. It is a second-order sort of effect – it might tip your very sensitive jetting over the edge, but it’s really hard to find circumstances where you need a normal standard jetting size change due to a small change in humidity. I include it here for completeness. It’s the most painful thing to calculate, too.
Calculating air density
The thing about those changes is how they interact – rarely does only one of those above parameters change. Here’s where things get a bit technical. I apologise for the maths, but it is required. I am going to do this by providing an example from Bureau of Meteorology observation data for Goulburn Airport (not far from Wakefield Park) for the time when I’m writing this article.
The relevant data are
Temperature: 13.1 ºC
Air pressure (MSL): 1035.2 hPa
Relative humidity: 55%
Altitude of station: 640.0 m
Note the air pressure thing – I’ve taken the MSL pressure. This is because I need the *ACTUAL* air pressure, and the BoM report both QNH and MSL pressures. MSL just happens to be something I can convert back to the actual air pressure rather than the air pressure that would be if you transplanted Goulburn at the current temperature down to sea level.
We need to do a couple of conversions. Temperature needs to be in Kelvin not ºC, but that’s easy:
We also need to convert the BoM pressure that we’d have at sea level back to the true air pressure. The equation to do that is as follows:
Obviously there’s a few constants we need in there :).
L is the rate at which temperature changes with respect to height in a standard atmosphere:
g is the acceleration due to gravity:
M is the molar mass of air:
R is the gas constant:
To simplify it a bit, I’ll calculate out that exponent, it comes to ~5.25578.
Now for the calcuation itself for our example:
That covers off the two things we need to convert to calculate density
Temperature: 291.25 K
Local true air pressure: 960.84 hPa.
Air density without humidity
Air density with humidity
That’s all well and good, but how the hell do I remember those numbers?
You don’t have to! That’s the point of working out the density in terms of ‘relative’ density numbers. These give you a percentage with respect to a ‘standard’ atmosphere (or you can set your own baseline, if you wish).
First, let’s calculate up the
Jetting based on RAD
Now we’re into
Calculators
These are coming, what I’m planning on doing are:
– Current RAD based on BoM data
– Current RAD based on your own data
– RAD & jetting changes from BoM against a baseline
– RAD & jetting changes from your own data
If you’d like to see other calculations or something like jetting table calculators, let me know via the FB group.